How to install nachOS on Ubuntu 11.04 (32 and 64 bits)

Reporte 5: Árboles binarios

Referencias:
Árboles binarios en Python
Árbol binario
Universidad Central de Venezuela -  árbol binario
Standford University - Binary tree
Animación de un árbol binario

-

Reporte 4: Lista simplemente enlazada

Reporte 3: DFS búsqueda de profundidad

Reporte 2: Problema de la mochila.

El problema de la mochila, tambien llamado knapsack problem, es un problema que modela la situación de llenar una mochila, limitada a cierta capacidad de peso y con cierta cantidad de objetos con diferentes pesos y valores cada uno. Los objetos que se pongan en la mochila deben de maximizar el valor total, sin superar el peso máximo permitido. Es uno de los 21 problemas NP-completos de Richard Karp.

El problema de la mochila: ¿Que cubos debemos elegir
 para maximizar la cantidad sin sobrepasar los 15 kg permitidos?

El problema de la mochila tiene sus puntos relevantes:

• Hay un algoritmo pseudo-polinomial (ya que ahora la salida es polinomial), con programación dinamica.
• Hay un aproximación de tiempo polinomial completo, utilizando el algoritmo anterior como subrutina
• El problema es NP-completo, por lo que se espera que ningún algoritmo puede ser rapido y correcto (en tiempo polinomial) en todos los casos.

Los datos del problema se pueden expresar en términos matemáticos. 

• Los objetos están numerados por el índice i variando de 1 a n. 
• Los números wi y pi representan el peso y el valor del número i. 
• La capacidad de la bolsa se denomina en esta formula W.

Existen muchas manera de llenar la mochila, para decidir a cada uno de ellos debemos de decir para cada objeto si lo metemos a la mochila o no, pudiendo utilizar el código binario que cuando xi = 1, metemos el objeto a la mochila, o xi = 0, se pone afuera, y para ir llenando esta mochila podemos utilizar un vector de contenido, que comprende: X = (x1, x2, ..., xn), entonces podemos expresar una función del contenido del vector.

Para un contenido dado X, el valor total de la bolsa es:

De la misma manera, la suma de los pesos de los objetos es:

El problema entonces lo podemos enunciar como un contenido de vectores X = (x1, x2, ..., xn), que tienen componentes de ceros y unos, teniendo como máximo la restricción de la función z(X).

Esto quiere decir que la suma de los pesos (o sea, la función w(X)), de los objetos que pusimos en la mochila no deben de superar la capacidad de esta, (o sea, la W).

Podemos decir que:

• z(X) es una función objetivo (como su nombre lo dice, representa el objetivo del problema, esta expresión se maximiza o se minimiza.
• Un vector X que cumple con la restricción W en la tercera formula se le nombra factible (o sea, que se pude hacer).
• Si tenemos un resultado máximo en z(X), entonces X es óptimo.

Se le pueden agregar otras restricciones según tengamos un caso, en esta liga, encontramos diferentes casos singulares.

Con esto podemos argumentar que tenemos un problema de decisión cuando para decidir a cada uno de ellos debemos de decir para cada objeto si lo metemos a la mochila o no, que cuando xi = 1, metemos el objeto a la mochila, o xi = 0, se pone afuera y podemos decir que es un problema de optimización porque podemos encontrar funciones objetivo, valores óptimos utilizando las declaraciones matemáticas.

El problema es NP-completo porque se puede representar como una toma de decisiones mediante el reemplazo del máximo, utilizando la siguiente pregunta: 

Dado el número k, existe un valor xi para el cual  

Existe un vinculo entre la version de decisión y la version de optimización del problema en que si existe un algoritmo polinomial que resuelve la versión de decisión,  por lo tanto, las dos versiones del problema son de dificultad similar.

El problema de optimización es NP-hard, su resolución es al menos tan difícil como el problema de decisión.

La prueba de que el problema es NP-completo fue presentado por Michail G. Lagoudakis, se puede encontrar en la misma liga

Algoritmos existentes:
Algoritmo Greddy o voraz: La idea es añadir un objeto prioritario mas efectivo hasta la saturación de la mochila. La complejidad de estos algoritmos se basa en la inversa de la calidad esperada.

Las dos fases del algoritmo voraz

Podemos ver las dos fases del algoritmo voraz.
      A) el ordenamiento de las cajas según un interes (en este caso en peso en $/kg)
      B) si es posible la entrar a la mochila.  




Algoritmo genético: se utiliza a menudo en problemas de optimización difíciles, como este, facil de implementar y obtener rapidamente una solución.

 

Ejemplo de la evolución de una población con
un algoritmo genetico.

Los objetos son utilizados para el algoritmo voraz, por ejemplo el genoma (0,1,0,0,0) corresponde a un cuadro de selección de 12 kg de peso 7.




Programación dinámica: El problema de la mochila tiene la propiedad que le permite utilizar el metodo de resolución de programación dinámica.
Este algoritmo tiene una complejidad en tiempo y espacio que tiene como ventajas la velocidad y no hay necesidad de ordenar las variables, pero como desventajas es que gasta mucha memoria, por lo tanto no puede ser solución para problemas grandes.

Aplicaciones en la vida real:

En la vida real, se utiliza para modelar diferentes situaciones:

• en los sistemas de apoyo a las fianzas: para encontrar el mejor equilibrio entre el capital y rendimiento financiero.
• en la carga del barco o avión: todo el equipaje debe ser llevado, sin ser sobrecargado.
• en el corte de materiales: para minimizar las caídas.
• entre otras...

Reducción:

El problema de la mochila, es un caso especial del SUBSET SUM, que viene de la reducción de 3-SAT, VERTEX COVER, en este PDF, vienen las reducciones hechas por Richard M. Karp de los 21 problemas, de la Universidad de Berkeley en los que se encuentra el problema de la mochila (knapsack). 

Referencias:

El Problema de la mochila, Universidad de Murcia. aqui.
Diapositivas de la clase: Optimización combinatoria. aqui.
Lecture: The knapsack problem. Technische Universiteit Eindhoven. aqui.
Reducibility among combinatorial problems de Richard M. Karp. aqui.
Encontré mucha información. aqui.

Este video me ayudó a entender la matemática, tiene subtítulos en español es del MIT.

Reporte 1: Algoritmo euclidiano.

El Algoritmo euclidiano es un algoritmo eficiente y popular para hallar el máximo común divisor de dos enteros.

El máximo común divisor de dos enteros (positivos y no sean 0) es el entero positivo más grande que divide a estos dos números, sin tener un residuo. Esto se utiliza, por ejemplo, para simplificar fracciones.

En la escuela nos enseñan un metodo para calcular el MCD, es descomponiendo los dos números en factores primos, esto quiere decir, sacando mitades o tercias etc...., luego marcamos cuando sean comunes divisores y estos al final se multiplican, esto es, por ejemplo:

Cuando nosotros dividimos entre a y b(números enteros positivos), nos dará como un resultados un cociente q y un residuo r, entonces como sabemos, r = a % b, por lo tanto mcd(a,b) = mcd(b,r); por ejemplo:

• Como 18 % 12 = 6, utilizando mcd(a,b) = mcd(b,r):
• mcd(18,12) = mcd(12,6)
• Como 60 % 48 = 12, utilizando mcd(a,b) = mcd(b,r):
• mcd(60,48) = mcd(48,12)

Algo importante que debemos considerar es que para obtener el MCD correcto tenemos que sacar el residuo dividiendo el mas grande entre el mas pequeño.

Considerando también que el máximo común divisor de cualquier numero y 0 es ese mismo numero, esto quiere decir:

• Como 80 % 40 = 0, utilizando mcd(a,b) = mcd(b,r):
• mcd(80,40) = mcd(40,0) = 40

Podemos ver que los resultados que obtuvimos con nuestro metodo que vimos en la escuela y el algoritmo euclidiano, en ambos obtuvimos el máximo común divisor.

Si a es un entero no negativo, b es un entero positivo y r = a mod b, entonces mcd(a,b) = mcd(b,r), decimos que, por el teorema de cociente-residuo: a = bq + r  y  0 <= r < b, este teorema es demostrado, donde a y b son los números dados, q es el cociente, r es el residuo.

El pseudocódigo de este algoritmo lo hice de esta manera:

Teniendo como entrada dos enteros no negativos, diferentes a cero y obteniendo como salida, el máximo común divisor de ellos.

El Diagrama de flujo para este algoritmo, es el siguiente:

Hay que notar se en este procedimiento utilizo las funciones XOR para intercambiar los datos dados por si en alguna ocasión se ingresa el menor y el mayor invertidos, también ver que los valores en el bucle while (mientras), se van actualizando con valores cada vez mas chicos, hasta que en algún momento b se vuelve 0, cuando en este punto mcd(a,0) por lo tanto es igual a a, que es el mcd.

Ahora mostraré como funciona por pasos este algoritmo en diferentes ocasiones.

Sean a = 48 y b = 60, entra a la condición ya que 48 < 60, pasamos a la siguiente linea numero 3 en donde con 3 XOR intercambio el orden para que a sea 60 y b sea 48, se hace lo siguiente.

• a = 48 XOR 60
• a = 12
• b = 12 XOR 60
• b = 48
• a = 12 XOR 48
• a = 60

Ahora estamos preparados para entrar el mientras, como b != 0, se hace lo siguiente.

• r = 60 % 48
• a = b
• a = 48
• b = r
• b = 12

Volvemos a entrar a el mientras y tenemos.

• r = 48 % 12
• a = b
• a = 12
• b = r
• b = 0

No entra al mientras y vamos a la linea 13 en donde regresa a a, que viene siendo el correcto MCD.

Hice un programa pequeño en C,  implementando el algoritmo:

Bibliografia:

MATEMATICAS DISCRETAS. Sexta edición.

Johnsonbaugh, Richard

PEARSON EDUCACION, México, 2005

Área: Universitarios.

PD. es el libro que utilizamos en la materia de Mates discretas, la pagina donde viene esta información es en la 205. Lo pueden conseguir en google books. en este link

Demostraciones finales

Implementacion

Aqui puedes descargar la documentación de mi proyecto.

Gracias!

Presentación final -Clase-

ProyectoFINAL

Implementación de interfaces gráficas -Taller-

Códigos documentados que implementan pantallas gráficas (5 puntos) con la funcionalidad correcta de los componentes ya incorporada (5 puntos)

Para realizar una aplicación para iOS se utiliza (regularmente) el patrón de diseño MVC
El cual separa los datos de una aplicación, la interfaz y la lógica en tres componentes.
Tambien es utilizado para aplicaciones en la WEB u otro tipo

• Modelo: Es la representación específica de la información con la cual opera el sistema.
• Vista: Presenta la interfaz gráfica
• Controlador: responde a los eventos.

Se puede encontrar de muchas maneras en este caso, el controlador y la vista van de la mano para conectarse con el modelo que viene siendo la lógica.


En resumen, cada capa se encarga de una tarea determinada, por lo que es mas facil identificar los códigos y encontrar errores por ejemplo si tenemos algún error no afecte a la lógica del sistema solo a la interfaz, o viceversa.


Capas de aplicación en imagenes:

Para esta entrada, presentaré los códigos de Menu y de Sucursales.
Para realizar la interfaz gráfica se utiliza la aplicación de interface builder, incluida en el SDK de desarrolladores de iOS, en esta aplicación se seleccionan los controladores que queremos y acomodarlos, existe tambien de manera de hacerlo como código, en mi proyecto las vistas que eran estáticas las realicé en interface builder y en código las que se iban a ir modificando.


Menu
Menu se divide en 2 subniveles, una que controla la tabla que aparece al principio y la otra que controla la pantalla de información, aparte de otro view que controla la celda de cada tabla ya que lo modifiqué para que apareciera imagenes.


En este caso RootViewController es el controlador de la raiz de Menu, el codigo esta comentado sobre las funciones que se generaron al seleccionar las clases correspondientes y el interface builder.

En interface builder seleccionamos que el RootViewController.xib este dirigido a el tab bar de Menu, luego de hacer esto arrastramos los controladores y hacemos las conexiones correspondientes.

Después lo que realicé es configurar aun mas la celda para poder ver información en ella, para eso hice otra clase que se dedicara unicamente a las celdas.

Solamente se declaran los IBOutlet y los conecto en interface builder para poderlos utlizar y en la funcion donde cambia de modo de ver la celda los utilizo para crear un objeto con ese tamaño y cambie segun la llave del objeto para luego que abra el .xib de la celda que lo realicé en interface builder.

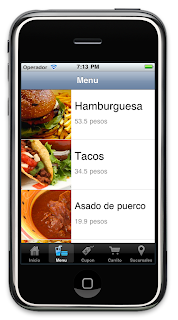
Y asi tenemos una vista como esta:

Luego para tener la información mas detallada al momento de seleccionar una de la celda realicé otro view controller.

Después, hice la interfaz en el builder arrastrando lo que necesito y luego conectar a la clase el cual contiene las características.

Tenemos una vista como esta:

Mapa

Para realizar la vista del Mapa utilicé IBActions para que al momento de que el usuario tocara, lo ubicara y muestre las sucursales disponibles, es importante decir que es necesario poner una clase Pin que hace uso de un patrón Builder para poder realizar las MKAnnotation.

// ACTUALIZAR CODIGO LUN 23 DE MAYO

En este código podemos ver las dos acciones que realiza los botones de Mapa.

Tenemos esta vista:

Ahora les anexo un video en donde pueden ver la implementación de la interfaz gráfica correctamente:

Diseño de interfaces gráficas -Clase-

Dibujos de diseños de pantallas que identifican los componentes utilizados, su posicionamiento y función

Componentes, posición, función:

La herramienta a utilizar fué interface Builder

Interface Builder

Mi aplicación esta hecha como una Tab Bar, la cual controla los diferentes xib cuyos archivos contienen los componentes utilizados de cada uno, en este caso en la Tab Bar le agregué 5 botones que tienen imagenes según el tema correspondiente, esas imagenes las descargué de aqui.

Para la interfaz principal.

• UILabels para poner los textos de la información.
• UIButton para poner por medio de un IBAction un botón para llamar desde el iPhone, en mi caso no funciona en el simulador.

Para la interfaz menu.

• UINavigation para poder hacer que la aplicación se desplace entre diferentes secciones (es la barrita azul de arriba).
• UITableView que es el que muestra toda la información extraída del plist cuyo contenido es la base de datos del restaurant.
• UITableViewCell es el que se dedica a poner otros componentes en la celda de menu, en este caso una imagen, nombre y precio.
• UIImageView esta contenido a un lado de la UITableViewCell, aparte cuando seleccionas una de estas celdas, esta misma imagen se muestra en la pantalla de descripción de la comida.
• UILabels contienen los nombres, precios y horas en las UITableViewCell y el View de descripción.
• UIPickerView es el que contiene la cantidad que deseas de producto.
• UITextView es el que contiene la descripción de la comida, tambien los lee de un plist.
• UIButton para comprar una comida.

Para interfaz cupones.

• UIImageView para mostrar los QRcodes, que se generaron en esta pagina.
• UILabels en medio de las imagenes con instrucciones.

Para sucursales.

• UINavigationBar para poner los dos botones sucursales y ubicación
• Bar Button Item para poner los dos botones de Ubicación y Sucursales, ubicación como su nombre lo indica te localiza en tu posición actual, y en sucursales te muestra por medio de MKAnnotation las coordenadas donde se encuentra una sucursales. 

Dibujos:

Sistemas distribuidos

Clase; 5 puntos

Texto con diagramas que explica la operación

 (incorporada o potencial) del software de manera distribuida

¿Que son sistemas distribuidos?
Son sistemas en los que elementos de hardware y software localizados en ordenadores en red, se transmiten y organizan sus operaciones, para así intercambiar mensajes, tambien podemos decir que es una recopilación de computadoras independientes ligados por una red y soportados por aplicaciones que producen que esta recolección se ejecute como un servicio integrado.




¿Que características lo identifican?

• Tolerancia a datos: ante un fallo el resto del sistema continua con sus operaciones.
• Transparencia: es cuando se oculta al usuario y al programador, separando los factores del sistema, por lo tanto este se observa como un todo, no como un conjunto de factores independientes.
• Concurrencia: cuando hay varios procesos (Programas que se ejecuta en una maquina) ejecutandose concurrentemente.
• Escalabilidad: operan de manera correcta y eficiente a diferentes escalas, esto quiere decir que puede tener en su estado mas pequeño dos estaciones conectados a un servidor de ficheros, uno adentro de una red de area local, podria tener cientos de estaciones y varios servidores.

¿Por qué sistemas distribuidos?

• Funcionales: los ordenadores tienen diferentes funciones u ocupaciones.
• Distribución del trabajo: los ordenadores se dividen las funciones.
• Económicos: es más barato.
• Físicos: en cualquier lugar del mundo.

En mi proyecto como un sistema distribuido...


Cliente-Servidor.
En mi proyecto se pudiera realizar un sistema distribuido cliente-servidor en donde el cliente seria el dispositivo y se solicita un servicio, luego, una maquina seria el servidor.


El cliente pide el menu con precios actualizados, y un servidor se los proporciona, al igual que si el cliente desea encargar la un platillo, que se conecte a un servidor a donde esta el restaurante y que este muestre los platillos en una lista, existen diferentes categorias de servidores, para mi proyecto se implementaria servidor de bases de datos para poder acceder al menu.


Tambien, se puede realizar cliente-servidor suponiendo que en la aplicación ya se tiene los datos pre-cargados (sobretodo si, para utilizar una función en el SDK que tiene para hacer una llamada a cierto numero, por si no tiene internet), luego este se conecte a un servidor que haga diferentes funciones, luego reciba una respuesta.


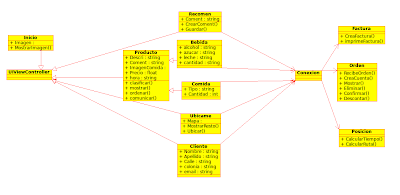
Un diagrama UML implementando esto seria:

Se utilizará asyncsocket que viene implmentado en el iPhone para poder realizar dichas operaciones.


Bibliografia
Introducción SD
Otra intruducción SD

Diseño de pruebas unitarias (Clase)

Clase: Semana 10 
Texto con diagramas que explica las pruebas unitarias a aplicar



¿Que son las Pruebas Unitarias?
Son como ensayos parara comprobar que funcionan diferentes partes del código, con estas pruebas podemos saber si nuestro proyecto esta fallando o no.


¿Porque hacer Pruebas Unitarias?

• Detectar y encontrar nuevos errores o bugs .
• Definir peticiones de cada función.
• Saber si un método es efectivo.
• Podemos aprobar un caso de estudio.
• No siempre se encuentran todos los errores.
• Separar la interfaz con la implementación.

De la iOS Development Guide nos dice que:
Xcode ofrece dos tipos de pruebas unitarias: pruebas de logica (Logic Tests) y pruebas de aplicación (Application tests).


Las pruebas de lógica son pruebas que verifican el correcto funcionamiento de nuestro código en un entorno "clean-room environment", esto quiere decir que el código no se ejecuta dentro de una aplicación, esto lo podemos utilizar para llevar a cabo pruebas en el código para asegurar que se comporta correctamente en situaciones en donde no estamos seguros como va a reaccionar nuestro programa, ayudan a hacer nuestro código robusto que funciona correctamente cuando se utiliza de maneras que no estamos anticipando, en xcode el código que se está probando se ejecuta durante la fase de "Builder".


Las pruebas de aplicación son pruebas que verifican la funcionalidad del código en una aplicación en ejecución. Debido a que las pruebas de aplicación se ejecutan en un solo dispositivo, también las podemos utilizar para realizar pruebas de hardware.


En mi proyecto, como explico en mi entrada de taller, por el momento realizo dos pruebas unitarias dentro de la clase MenuTestCase, aqui expongo mi diagrama de clases actualizado con la clase de las pruebas unitarias incluida, podemos ver la clase MenuTestCase, que hereda de SenTestCase

Mi diagrama UML

OCUnit
OCUnit es un framework de pruebas para Objective C en Mac OS X integrado con xcode. Podemos probar los frameworks, paquetes o aplicaciones y es basado en SUnit para Smalltalk y en JUnit para Java.


Incluye un framework "SenTestingKit" que nos ayuda a escribir casos de prueba, teniendo como ventajas que podemos implementar pruebas en el mismo Objective C y tiene una integración total con xcode.


Para descargar OCUnit aqui.


Usando OCUnit en mi proyecto..
Luego de instalar OCUnit, descargado de la pagina.


1. Necesitas agregar un nuevo "Unit Test Bundle".

2. Le pones un nombre al target y das Next..

3. Luego se modifica "Other linker flags" cambiando de Cocoa a Foundation, esto para permitir que compile en el iPhone simulator.

4. Buscas Cocoa.h y borras las referencias.

5. Agregas una nueva clase en el proyecto "Objective-C test case class"

6. Es importante que al final del nombre de la clase se llame TestCase y seleccionas el nombre del Target.

7. Todos los metodos deben empezar con test

8. Agregas el Target a los metodos que los necesitas probar.

9. Es importante que cuando quieras hacer el Build, necesitas activar el Target.

Cualquier duda o pregunta sobre la entrada, pueden comentar.

Pueden encontrar mas información en los siguientes enlaces.

Integrated Unit Testing

Your Code with OCUnit